

So let’s say the tire of a car, every time it turns is another 360 degrees. Now, let’s think about something mechanical, say the tire of a car. Well if I turn around three times, how much angle have I turned through? I’ve turned through 1,080 degrees of angle, okay? That just something simple I can do with my body. I could turn around once, or if I’m feeling really ambitious, I could turn around three times. And we can see in the real world obtuse angles, we could have an obtuse angle between three points on a map, that sort of thing.
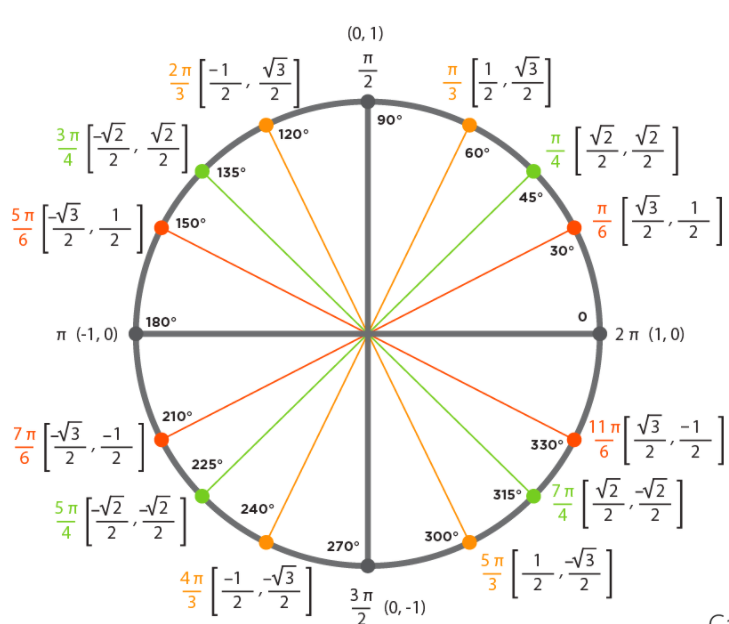
There’s are all kinds of geometric shapes. First of all, there are certainly architectural features that can have obtuse angles. In the real world there many angles that are outside of that range, so consider the following. And that’s a quite limited range if you think about it, because angles can be much much bigger than that. And of course, in a right triangle, the acute angles must be bigger than 0 degrees, and smaller than 90 degrees. That’s all we’ve talked about, SOHCAHTOA and right triangles. In the previous videos we’ve just talked about SOHCAHTOA in right angles. Expansion of Trig: The Unit Circle ContextĪnd so I’m assuming at this point you’re comfortable with SOHCAHTOA, and that’s going to be our jumping off point. So that’s what we’re gonna talk about in this lesson. One of the most elegant examples of this in all of mathematics, it’s really actually incredible in the greater view of mathematics–is simply expanding trigonometry from the limited SOHCAHTOA context, to the much more inclusive unit circle context. Is that once mathematicians had figured out how something works in a limited context, the next step is always to consider how the idea can be expanded to a broader context.Īnd that’s exactly what we’re gonna do in this video. So, first I’ll say that one of the far ranging patterns in mathematics, this is big picture. This is where trigonometry really gets interesting.


 0 kommentar(er)
0 kommentar(er)
